Fibonacci numbers

0 1 1 2 3 5 8 13 21 34 55 89 .....

เอ...แล้วเลขอะไรต่อน้า...

อ้อ ช่ายแล้ว 144 ครับ

ความสัมพันธ์ของเลขชุดนี้ก็คือ เลขตัวต่อไป เป็นผลบวกของเลขสองตัวก่อนหน้า หรือเขียนในรูปอนุกรมได้ว่า F(n+1)=F(n)+F(n-1)

อืม แล้วมันทำไมเหรอครับ ก็เขาว่ากันว่าเจ้าเลขชุดนี้เนี่ย เป็นเลขชุดที่มหัศจรรย์ที่สุด สวยงามที่สุด และแปลกประหลาดที่สุดเลยทีเดียวละครับ และเราจะพบเจ้าเลขชุดนี้ และ limit ของมันทั้งในธรรมชาติ ต้นไม้ ดอกไม้ ศิลปะ ภาพถ่าย สถาปัตยกรรม รวมไปถึงร่างกายของเราซะด้วย

เชื่อไหมละครับ ว่ามีวารสารทางคณิตศาสตร์เพื่อศึกษาเจ้าเลขชุดนี้โดยเฉพาะเลยทีเดียว ชื่อ The Fibonacci Quarterly

มันเป็นยังไงเหรอครับ อ่ะ เริ่มฟังน่าสนใจยังครับ เอ้า ล้อมวงเข้ามาอีกทีครับ ผมจะเล่าให้ฟัง

เจ้าเลขชุดนี้โด่งดังมาจาก นักคณิตศาสตร์ชาวเมือง Pisa คนนึง ชื่อ Leonardo of Pisano หรือ Fibonacci (ซึ่งแปลว่า ลูกของนาย Bonacci) เขาเขียนเรื่องเกี่ยวกับเจ้าเลขอนุกรมนี้ไว้ในหนังสือชื่อ Liber Abaci (แปลว่า Book of the Abacus or Book of Calculating ครับ) ตั้งแต่สมัยต้นคริสตศตวรรษที่ 13 นู้น

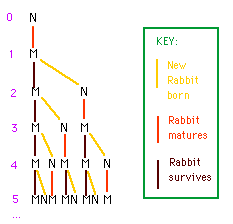เขาตั้งคำถามว่า ถ้าคนเลี้ยงกระต่ายคนหนึ่งมีกระต่ายอยู่หนึ่งคู่ ถ้าเวลาผ่านไปเรื่อยๆ เขาจะมีกระต่ายทั้งหมดกี่คู่ ถ้ากระต่ายออกลูกมาเดือนละหนึ่งคู่ และกระต่ายใช้เวลาสองเดือนถึงจะออกลูกครั้งแรกได้ และสมมุติกระต่ายเหล่านี้เป็นกระต่ายพลังม้า เมื่อครบสองเดือนกระต่ายแต่ละคู่จะออกลูกทุกเดือน เดือนละหนึ่งคู่ และไม่ตายเลย (และกระต่ายเหล่านี้เป็นกระต่าย ผัวเดียวเมียเดียวนะครับ)

จะเห็นได้ว่าจำนวนกระต่ายออกมาเป็นอนุกรมที่อ้างไว้ข้างบน คือ 1 1 2 3 5 8 13 ... และ ถ้าสังเกตดีๆจะพบว่า จำนวนกระต่ายในเดือนนี้ จะเท่ากับผลบวกของจำนวนกระต่ายสองเดือนก่อนหน้าพอดี....

แต่ไม่ได้หมายความว่า นาย Fibonacci เป็นคนค้นพบเลขชุดนี้นะครับ ว่ากันว่า ก่อนหน้าที่นาย Fibonacci จะตีพิมพ์งานนี้ ก็มีนักคณิตศาสตร์ชาวอินเดีย พูดถึงเจ้าเลขชุดนี้แล้ว

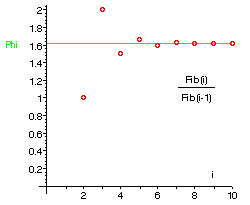ถ้าเอาเลขแต่ละตัวหารด้วยตัวก่อนหน้ามัน จะพบว่า สัดส่วนนี้มัน converge ครับ ใครเคยเรียน `ดิฟอีเควฯ' มาคงบอกว่า หมูๆ ก็แค่สมมุติให้ lim F(n)/F(n-1)=L แล้วเอา F(n) หารอนุกรมข้างบน จะได้ F(n+1)/F(n)=1+F(n-1)/F(n) อัด lim เข้าไป จะได้ L=1+1/L หรือ L^2-L-1=0 แก้สมการนี้ ได้ L=(1+sqrt(5))/2 กับ (1-sqrt(5))/2 หรือ ประมาณ 1.6180339887 (เอาแค่ค่าบวกอย่างเดียว) เขาเรียกเจ้า limit นี้ว่า Phi (ไฟใหญ่) ครับ

ความมหัศจรรย์อันแรกคือ 1/Phi=0.6180339887 อ๊ะ ทำไมเลขหลังจุดทศนิยมมันเหมือนกันหมดเลย ไม่น่าเชื่อ (จริงๆแล้วใครดูสมการข้างบนดีๆก็คงพอรู้ว่ามันมาได้ไง) เขาเรียกเจ้าค่านี้ว่า phi (ไฟเล็ก) ครับ

ฟังๆดูอาจรู้สึกว่า มันก็เลขอนุกรมธรรมดาๆชุดนึง เดี๋ยวผมจะเล่าให้ฟังครับ ว่ามันไม่ธรรมดายังไง

ว่ากันว่าเจ้าเลขชุดนี้เนี่ยพบได้ทั่วไปในธรรมชาติครับ

ก่อนอื่น ลองเอาสี่เหลี่ยมจตุรัสขนาด 1x1 มาต่อกัน แล้วเอาสี่เหลี่ยมจตุรัสอีกอันมาประกบด้านยาว แล้วเอาสี่เหลี่ยมจตุรัสมาโปะอีกไปเรื่อยๆ เราจะพบว่าขนาดของสี่เหลี่ยมจตุรัสที่เราเอามาต่อ จะมีขนาด 2x2 3x3 5x5 8x8 13x13 21x21 .... เอ เลขชุดนี้คุ้นๆไหมครับ แล้วถ้าเราลาก quarter ของวงกลมภายในสี่เหลี่ยมแต่ละรูปเหล่านี้ เราจะได้รูปข้างล่างครับ



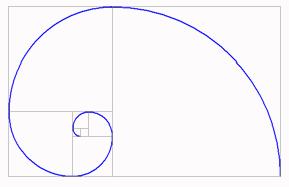
เอ..มันรูปอะไรนะ คุ้นๆ



ช่ายแล้วครับ เปลือกหอยนั่นเอง

นอกจากนี้ นักคณิตศาสตร์ว่างงาน ที่ชอบศึกษารูปแบบของพืช (ศาสตร์การศึกษารูปแบบของพืชพวกนี้ เรียกว่า Phyllotaxis ครับ ใครสนใจลองกดเข้าไปดูได้ครับ สนุกดี) ยังไปนั่งจ้องดอกกระหล่ำ เกสรดอกทานตะวัน ลูกสน หรือแม้กระทั่ง สับปะรด แล้วพบว่า เจ้าพืชพวกนี้ส่วนใหญ่ (ไม่ใช่ทั้งหมดนะครับ) มีจำนวนเกลียว (หรือ spiral) เท่ากับเจ้าเลข fibonacci เสียด้วย (ผมก็บ้าไปจ้องกับเขามาแล้วครับ)

ลองดูกันเล่นๆครับ ที่บ้านใครมีดอกกระหล่ำ ลูกสน หรือสับปะรด ลองไปหยิบมาดูนะครับ

เขาบอกว่า ถ้านับจำนวนเกลียวของเจ้าดอกกระหล่ำลูกนี้ วนไปทางขวา จะได้ 5 เกลียวครับ ดูออกไหมครับ ถ้าไม่ออกลองกดปุ่มนี้ดูสิครับ
อ่ะ แล้วนับเกลียววนซ้ายบ้าง นับได้ 8 เกลียวครับ ดูไม่ออกเหรอครับ กดปุ่มข้างล่างนี้ดูครับ
หนุกดีครับ ว่างๆไปนั่งนับดูนะครับ (อันนี้ลอกมาจาก http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html ครับ

นอกจากนี้แล้ว ยังพบอีกว่า จำนวนกลีบดอกไม้ จำนวนยอดของต้นไม้ ความยาวของต้นไม้ ยังสอดคล้องกับเจ้าเลขชุดนี้อย่างประหลาด ลองไปดูที่เวบนี้สิครับ บางอันผมว่าเป็นเรื่องบังเอิญนะ แต่ดูแล้วก็น่าสนใจไม่น้อยทีเดียว

ยังครับ ยังไม่หมด

เจ้าเลขชุดนี้ และลิมิตของมันยังถูกพบเห็นทั่วไปในงานศิลปะ สถาปัตยกรรม และดนตรีอีกด้วย

ถ้าใครเคยถ่ายรูป หรือวาดภาพ คงจะชินกันกฎ rule of third หรือจุดตัดเก้าช่องเป็นอย่างดี ท่านผู้รู้เขาบอกไว้ว่า เวลาเราจัดองค์ประกอบของรูป อย่าเอาจุดสนใจ หรือขอบฟ้าไว้ตรงกลางภาพเด๊ะ ให้ลองลากเส้นแบ่งรูปออกเป็น 9 ส่วน แล้วพยายามเอาจุดสนใจของภาพไว้ตรงจุดตัดของเส้น

มีคนบอกครับ ว่าไอ้ rule of third เนี่ย มาจากเจ้าเลขชุดนี้นี่เอง เชื่อไหมละครับ

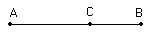สมมุติว่าเรามีเส้นตรงเส้นนึง เราจะแบ่งเส้นตรงเส้นนี้ออกเป็นสองส่วนยังไง โดยให้ AC:CB=AB:AC?

ลองคิดเล่นๆดูจะพบว่า เจ้าอัตราส่วนที่ได้มาเนี่ยคือ 1.618... หรือ เจ้าไฟใหญ่ที่เราเจอข้างบนพอดี และเราจะได้ส่วน AC:AB=phi หรือเจ้าไฟเล็กนี่เอง(ลองไปคิดเป็นการบ้านนะครับ ว่าออกมากลายเป็นไฟใหญ่ได้ยังไง)

ว่ากันว่าไอ้เจ้าอัตราส่วนนี้เนี่ย เป็นการแบ่งเส้นตรงที่ "สวยงามที่สุด" แต่บังเอิญว่า เจ้าไฟเล็ก หรือ 0.618 เนี่ย ใกล้เคียงกับ 2/3 เขาเลยตั้งเป็นกฎง่ายๆว่า rule of third ซะเลย

พบว่ามีการใช้เจ้าอัตราส่วนนี้ในงานศิลปะเต็มไปหมด ตั้งแต่สมัยก่อน ทั้ง ปิรามิดที่อียิปต์ วิหาร Parthenon Leonardo da Vinci ถึงกับเรียกเจ้าอัตราส่วนนี้ว่า "อัตราส่วนทอง" (golden ratio, golden section) เลยครับ Leonardo da Vinci เองก็ใช้เจ้าอัตราส่วนนี้ในภาพวาดหลายๆภาพของเขา ส่วน Luca Pacioli นักคณิตศาสตร์ยุค renaissance เรียกเจ้าสัดส่วนนี้ว่าว่า the Divine Proportion เลยทีเดียวครับ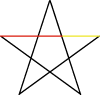

ยังมีเจ้าสัดส่วนนี้อยู่รอบๆตัวเราอีกครับ ถ้าวาดรูปดาวห้าเหลี่ยมด้านเท่า ลองเดาสิครับว่าอัตราส่วนระหว่างสีทองกับสีแดงในรูปจะออกมาเป็นเท่าไร

ลองหยิบบัตรเครดิตในกระเป๋าตังค์ออกมาแล้ววัดขนาดด้านยาวกับด้านสั้น ลองหารกันดู แล้วเดาสิครับว่าจะได้อัตราส่วนใกล้เคียงกับอะไร?

ยังอีกครับ ยังไม่หมด คนช่างสังเกตยังบอกอีกครับ เรายังเจอเจ้าอัตราส่วนนี้ในตัวของเราเองอีกครับ ทั้งใบหน้า ขนาดของร่างกาย มือและนิ้ว หรือแม้แต่ขนาดของเกลียว DNA! เวอร์หรือเปล่าไม่รู้ครับ ไปดูกันเอาเอง (โปรดใช้วิจารณญาณในการรับชม)


อ่านมาจนจบเริ่มรู้สึกว่า เหมือนอ่าน conspiracy theory หรือเปล่าครับ (ใครอ่าน Da Vinci's Code คงรู้สึกว่าคุ้นๆ) ทั้งหมดจะเป็นเรื่องบังเอิญหรือเปล่าก็ไม่แน่ แต่ผมว่ารอบๆตัวเรา มีคณิตศาสตร์วนๆอยู่มากกว่าที่เราคิดนะครับ

ถ้าสนใจเกี่ยวกับคุณสมบัติทางคณิตศาสตร์ของเจ้าไฟใหญ่กับไฟเล็ก และเรื่องอื่นๆเกี่ยวกับ Fibonacci ไปอ่านเพิ่มเติมได้ที่นี่
ครับ http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/

เพิ่มอีกหน่อยครับ เพิ่งเห็นเวบนี้ http://www.goldenmeangauge.co.uk/golden.htm ลองไปดูสิครับ ว่าเรื่องจริงหรือบังเอิญ